We are back from holidays, where we entertained ourselves with home-made Peano numbers and home-made Binary numbers, and back to optimising a hash-based program, namely the implementation of the Conway’s Game of Life.
Here is a quick recap of what we were doing before:
- In “Game of Life, hash tables and hash codes” we implemented Life in Java using hash maps. We ran the program on the
ACORNpattern:
and measured time for 10,000 steps. The first result we achieved was 2763 ms, or 3619 frames/sec on Java 7.
-
In the same article we discovered that the speed depends big time on the choice of the hash function. We found several that work reasonably well, the best one being based on calculating a remainder when dividing by a big prime number. The times achieved using this function were 1890 ms using Java 7 and 1550 ms using Java 8. The times went up to 2032 ms and 1650 ms later during refactoring.
-
Then we spent some time measuring and disassembling the hash function and took interesting detours into optimising division, performing multiplication using Karatsuba’s method, optimising CRC32 and doing some JNI work. Neither of these improved the speed – the original implementation of a division-based function in Java was the best.
-
In “Optimising the hash-based Life” we performed several optimisations of the main program, mostly based on the idea of replacing the Java standard classes with a custom code. The times achieved were 1020 ms on Java 7 and 904 ms on Java 8.
-
Finally, in “Choosing the hash map’s capacity” we studied dependency of performance on the declared capacity of the hash map and discovered that collecting hash maps elements into a linked list (which is done by
LinkedHashMap) improves iteration speed and allows using much higher capacity. The best results were achieved on capacity 512K – 843 ms for Java 7 and 581 ms for Java 8. The latter result corresponds to the Life simulation speed of 17,500 frames/sec.
Here are all the results in a table:
| Class name | Comment | Time, Java 7 | Time, Java 8 |
|---|---|---|---|
| Hash_Reference | Original version, original hash function | 2763 | 4961 |
| Hash_LongPoint | Original version, modulo-based hash function | 2032 | 1650 |
| Hash7 | ArrayList replaced with an array | 1020 | 904 |
| Hash8 | LinkedHashMap used, capacity made bigger | 843 | 591 |
Home-made hash table
Some of the improvements achieved so far were caused by re-writing standard Java classes with those of our own, specially designed for the purpose. We replaced Integer
with our own mutable class, then Long with a class with custom hash function, and finally ArrayList with an ordinary array. Now it’s time to look
at the HashMap class itself.
The HashMap class (and its parent AbstractMap) is big, but that’s because it provides a lot of functionality – iterators, key and value sets, resizing, checks for
concurrent modifications, workarounds for poor quality hash functions, and a lot more. The basic hash map functionality is simple and can be easily reproduced by hand (in the old days
of plain C that’s what programmers did: implemented each hash map by hand). But why do it, what’s wrong with the default implementation?
The default implementation maintains an array of chains, each chain being a linked list of Entry objects (in Java 8 long chains are converted into binary trees,
which complicates the code a lot). Each Entry object contains a reference to the key object (LongPoint in our case) and a reference to the value object (Value in our case).
This makes it three objects per data element, and, when implementing it by hand, we can get away with one object only, containing both key and value (in which case the
key may be stored simply as long). Moreover, this way we also save a call to equals on the key objects: we can compare long values directly. Altogether this offers
some improvement, we’ll check now how big.
All the code is available in this repository.
First, we need an object to replace Entry, we’ll call it Cell:
public final class Cell
{
final long position;
int index;
int neighbours;
boolean live;
Cell table_next;
public Cell (long position, int neighbours, boolean live)
{
this.position = position;
this.neighbours = neighbours;
this.live = live;
}
public Cell (long position, int neighbours)
{
this (position, neighbours, false);
}
public Point toPoint ()
{
return LongUtil.toPoint (position);
}
public void inc ()
{
++ neighbours;
}
public boolean dec ()
{
return --neighbours != 0;
}
public void set ()
{
live = true;
}
public void reset ()
{
live = false;
}
}This is a slightly upgraded version of Value. It contains key data (position), value data (neighbours and live) and the Entry artefacts (index and table_next).
The HashMap.Entry has field hash, which is used to speed up comparisons: the keys in the same chain may have different hash codes, so it makes sense to compare these
codes first, before invoking equals. In our case equals is replaced with a direct check of position, which is a primitive operation and does not require checking hash
first. So we don’t need to keep hash code; instead, we’ll store the index in the array, to be used in remove operation.
Now we make a class Field to implement the new hash map:
public final class Field
{
public static abstract class Action
{
public abstract void perform (Cell cell);
}
private final Cell[] table;
private final Hasher hasher;
private int count = 0;
public Field (int capacity, Hasher hasher)
{
table = new Cell [capacity];
this.hasher = hasher;
}
public void clear ()
{
for (int i = 0; i < table.length; i++) {
table [i] = null;
}
}
private int hash (long key)
{
return hasher.hashCode (key);
}
private int index (int hash)
{
return hash & (table.length - 1);
}
public Cell get (long key)
{
for (Cell c = table [index (hash (key))]; c != null; c = c.table_next){
if (c.position == key) {
return c;
}
}
return null;
}
public void put (Cell cell)
{
int index = cell.index = index (hash (cell.position));
cell.table_next = table [index];
table [index] = cell;
++ count;
}
public void remove (Cell cell)
{
int index = cell.index;
if (table [index] == cell) {
table [index] = cell.table_next;
-- count;
return;
}
for (Cell c = table [index]; c != null; c = c.table_next) {
if (c.table_next == cell) {
c.table_next = cell.table_next;
-- count;
return;
}
}
}
public void iterate (Action action)
{
for (Cell cell : table) {
for (Cell c = cell; c != null; c = c.table_next) {
action.perform (c);
}
}
}
public int size ()
{
return count;
}
}Some comments:
-
The
putandremovecalls only takeCellobject, they do not need separate key parameter. -
The
gettakes alongparameter, so we don’t need to create a key object just to be used as a method parameter. -
We still need to give the system a hash code calculator. Previously, it was a part of a key object; now it is a parameter of a
Fieldclass itself, and it is specialised to uselong, rather than some class. -
The main
Lifeimplementation asks for the table size when allocating temporary arrays; that’s why theFieldclass must maintain this value -
This implementation does not support table resizing. We can introduce it later. Alternatively, we can set the table capacity to some very big value.
The iterator deserves a few words, as this is a problematic point in the general collection design. There are three ways to arrange iteration of the data structure:
-
Using an iterator object, or, if only one iteration at a time is allowed, using the collection itself as such an object. This makes it easy to use the iterator, but difficult to develop it, for it must keep its entire state in its fields and be able to move forward from each point.
-
Using a call-back. This makes it easy to create an iterator, but more difficult to use it – now the client’s program must keep its context in fields.
-
Combine the best of the first two approaches by running the iterator and the client program in two threads or co-routines with some sort of data transfer between them. This makes it easy for both sides, but usually much less efficient, unless supported directly by the hardware. This approach is very popular among Go programmers.
We’ve used the approach 2. Possibly, we’ll later consider removing the call-back.
The Life implementation (class Hash_HomeMade) can be seen in the repository. It doesn’t differ much from the previous version (Hash8). Here is an example. Previously,
inc() method looks like this:
private void inc (long w)
{
LongPoint key = factory.create (w);
Value c = field.get (key);
if (c == null) {
field.put (key, new Value (1));
} else {
c.inc ();
}
}Now it looks like this:
private void inc (long w)
{
Cell c = field.get (w);
if (c == null) {
field.put (new Cell (w, 1));
} else {
c.inc ();
}
}We got rid of a key factory, which is good. This factory was introduced during the program refactoring (in “The fun and the cost of refactoring”), and back then it damaged performance a bit. Now we’ve recovered.
Here are the new times:
| Class name | Comment | Time, Java 7 | Time, Java 8 |
|---|---|---|---|
| Hash8 | LinkedHashMap used, replaced with an array | 843 | 591 |
| Hash_HomeMade | The first home-made hash map implementation | 513 | 465 |
We got some improvement, so the idea of replacing standard classes with specialised ones has value.
Getting rid of call-backs
The call-back in iterate() looks ugly; it helps writing generic code, but if this was our objective, we could have stayed with the standard Java hash maps.
Let’s get rid of it. And the only way to get rid of it is to pull all the code from Field right inth Hash_HomeMade – see Hash_HomeMade2.
We keep methods get, put and remove, but inline iterate straight into the code of step. Previous code looked like this:
field.iterate (new Field.Action() {
@Override
public void perform (Cell cell)
{
if (cell.live) {
if (cell.neighbours < 2 || cell.neighbours > 3)
toReset[resetPtr ++] = cell;
} else {
if (cell.neighbours == 3) toSet[setPtr ++] = cell;
}
}
});Now it looks like this:
for (Cell cell : table) {
for (Cell c = cell; c != null; c = c.table_next) {
if (c.live) {
if (c.neighbours < 2 || c.neighbours > 3) toReset[resetPtr ++] = c;
} else {
if (c.neighbours == 3) toSet[setPtr ++] = c;
}
}
}The new code has fewer lines but is less descriptive. Let’s see if it runs faster:
| Class name | Comment | Time, Java 7 | Time, Java 8 |
|---|---|---|---|
| Hash_HomeMade | The first home-made hash map implementation | 513 | 465 |
| Hash_HomeMade2 | The hash map code is built into the main code | 479 | 449 |
There is some improvement again.
Listing the cells
We are currently using the hash map capacity of 8192, with no resizing implemented. This is cheating, since we know this hash map capacity is good enough for the configuration we are testing with – but what if some other configuration requires bigger hash map? We could increase the hash map capacity, but, as we know from “Choosing the hash map’s capacity”, this may make iteration very slow, unless we collect all the hash map elements into some easily iterable collection, such as a linked list. That’s what we’ll do now. Since we need to remove arbitrary elements from this list, it will be double-linked.
First, we make a new class, called LinkedCell, which adds two extra links to a Cell:
public final class ListedCell
{
final long position;
int hash;
int neighbours;
boolean live;
ListedCell table_next;
ListedCell next;
ListedCell prev;
// ....
}This is why we called the link to the next element in the chain table_next – in anticipation that we’d need a simple next for something else.
We now need the head of the list (see Hash_HomeMade3):
ListedCell full_list;
public Hash_HomeMade3 (Hasher hash)
{
this.hasher = hash;
this.name = getClass().getName () + ":" + hash.getClass ().getName ();
this.table = new ListedCell [HASH_SIZE];
full_list = new ListedCell (0, 0);
full_list.prev = full_list.next = full_list;
}and methods to manipulate the list:
private void add_to_list (ListedCell cell)
{
cell.next = full_list.next;
cell.next.prev = cell;
cell.prev = full_list;
full_list.next = cell;
}
private void remove_from_list (ListedCell cell)
{
cell.next.prev = cell.prev;
cell.prev.next = cell.next;
}The calls to these methods must be added to put and remove.
Finally, the new iterator:
for (ListedCell cell = full_list.next; cell != full_list; cell = cell.next) {
if (cell.live) {
if (cell.neighbours < 2 || cell.neighbours > 3)
toReset[resetPtr ++] = cell;
} else {
if (cell.neighbours == 3) toSet[setPtr ++] = cell;
}
}Here are the new results:
| Class name | Comment | Time, Java 7 | Time, Java 8 |
|---|---|---|---|
| Hash_HomeMade2 | The hash map code is built into the main code | 479 | 449 |
| Hash_HomeMade3 | The cells are collected into a double-linked list | 480 | 433 |
It got slower on Java 7, but improved on Java 8.
Playing with the hash map capacity
Now, as we introduced the list, we can make the hash map capacity bigger. We could run the full study here, comparing performance on all possible values, but, as I mentioned before, small values involve some degree of cheating, so let’s concentrate on higher values - around one million.
| Capacity | Java 7 | Java 8 |
|---|---|---|
| 8192 | 480 | 433 |
| 256K | 405 | 353 |
| 512K | 419 | 369 |
| 1M | 417 | 381 |
| 2M | 433 | 415 |
All the values look good, the best being 256K. We’ll use this value (see Hash_HomeMade4) and keep in mind that we may need to increase it for bigger structures,
in which case 1M or 2M would also work.
The action lists
The operations with the action arrays (toSet and toReset) look very ugly. The way these arrays are allocated (way above the really needed size), the fact that they
must be allocated upfront and maintained – all of that doesn’t look nice. What if we collect the cells into some other data structure? It is worthwhile even just for
aesthetic reasons, but it may improve performance as well. Let’s collect the cells into two linked lists toSet and toReset. To do this, we’ll introduce a new type of cell,
called ActionCell, with a new field:
ActionCell next_action;The step() method is modified in the following way:
public void step ()
{
ActionCell toSet = null;
ActionCell toReset = null;
for (ActionCell cell = full_list.next; cell != full_list;
cell = cell.next)
{
if (cell.live) {
if (cell.neighbours < 2 || cell.neighbours > 3) {
cell.next_action = toReset;
toReset = cell;
}
} else {
if (cell.neighbours == 3) {
cell.next_action = toSet;
toSet = cell;
}
}
}
ActionCell next_action;
for (ActionCell c = toSet; c != null; c = next_action) {
set (c);
next_action = c.next;
c.next_action = null;
}
for (ActionCell c = toReset; c != null; c = next_action) {
reset (c);
next_action = c.next;
c.next_action = null;
}
}Note the two last loop structures. We want to clear the next_action pointers to improve garbage collection: we don’t want the removed cells to be available via these pointers from
some other cells that are still alive.
Here are the results:
| Class name | Comment | Time, Java 7 | Time, Java 8 |
|---|---|---|---|
| Hash_HomeMade4 | The hash map capacity is set to 256K | 405 | 353 |
| Hash_HomeMade5 | The action lists were introduced | 395 | 354 |
The lists made it better on Java 7 and almost made no difference on Java 8.
Other hash functions
Apart from the hash function we are currently using (based on division) we previously got good results using two hash functions based on multiplications. Let’s try them:
private static class Hasher4 extends Hasher
{
public int hashCode (long key)
{
return (hi(key) * 1735499 + lo(key) * 7436369);
}
}
private static class Hasher5 extends Hasher
{
public int hashCode (long key)
{
long x = key * 541725397157L;
return lo(x) ^ hi(x);
}
}| Class name | Comment | Time, Java 7 | Time, Java 8 |
|---|---|---|---|
| Hash_HomeMade5:Hasher6 | The division-based hash function | 395 | 354 |
| Hash_HomeMade5:Hasher4 | Multiplication by two big numbers | 425 | 367 |
| Hash_HomeMade5:Hasher5 | Multiplication by one big number | 426 | 381 |
The division-based function looks the best, probably due to its slightly higher quality of hashing
Statically defined hash function
We still have one more option: to replace the configurable hash code with the hard-coded one. We’ll remove the Hasher parameter and put the division-based code straight
into hash() method:
| Class name | Comment | Time, Java 7 | Time, Java 8 |
|---|---|---|---|
| Hash_HomeMade5:Hasher6 | The division-based hash function | 395 | 354 |
| Hash_HomeMade6 | The division-based hash function, hard coded | 392 | 353 |
Additive hash functions
Since hash functions must spread the values as wide across the table as possible, intuitively it seems that they must behave as close to random functions as possible.
This specifically discourages any predictive behaviour – ideally, it should be very difficult to calculate hash(x+1) given the value hash(x). Strangely enough,
our functions are not like that. Both division-based function (class Hasher5) and the one based on multiplying by two big numbers (Hasher4) allow easy calculation
of a hash code for a neighbouring cell given a hash code of the cell itself. We can try exploiting this fact to avoid calculation of the hash function where its value can
be obtained by updating some previous value.
First, we’ll need a version of the ActionCell that stores hash value rather than index (see HashCell.java). It will set this value in the constructor. The initial cells
will get this value from real invocation of the hash function. All the others are created because they were neighbours for some other cells, and they can get the hash value
by appropriately updating their hash value. This is what it looks like for the remainder-based hash (see Hash_Additive):
public static final int BASE = 946840871;
public static final int A = (int) (0x100000000L % 946840871);
public static final int B = 1;
private int hash (long key)
{
return (int) (key % BASE);
}
private int add_hash (int hash, int v)
{
hash += v;
if (hash > BASE) hash -= BASE;
return hash;
}
private int sub_hash (int hash, int v)
{
hash -= v;
if (hash < 0) hash += BASE;
return hash;
}
private void inc (long w, int hash)
{
HashCell c = get (w, hash);
if (c == null) {
put (new HashCell (w, hash, 1));
} else {
c.inc ();
}
}
void set (HashCell c)
{
long w = c.position;
int h = c.hash;
inc (w-DX-DY, sub_hash (h, A+B));
inc (w-DX, sub_hash (h, A));
inc (w-DX+DY, sub_hash (h, A-B));
inc (w-DY, sub_hash (h, B));
inc (w+DY, add_hash (h, B));
inc (w+DX-DY, add_hash (h, A-B));
inc (w+DX, add_hash (h, A));
inc (w+DX+DY, add_hash (h, A+B));
c.set ();
}This way we replaced calculation of remainder (which is in fact implemented as two multiplication) with one addition and one check. Fortunately, in each case we know if it is the upper or the lower boundary that we must check.
Note that this strategy works well because the key is never negative.
Another hash function that allows easy additive implementation is Hasher4:
private static class Hasher4 extends Hasher
{
public int hashCode (long key)
{
return (hi(key) * 1735499 + lo(key) * 7436369);
}
}Modification of x and y co-ordinates causes appropriate modification of the hash value, we don’t even need any checks (see Hash_Additive2). This may allow the solution
based on this hash to outperform the remainder-based solution, which, as we know, is faster.
Here are the results:
| Class name | Comment | Time, Java 7 | Time, Java 8 |
|---|---|---|---|
| Hash_HomeMade6 | The division-based hash function, hard coded | 392 | 353 |
| Hash_Additive | The division-based hash function, additive | 358 | 327 |
| Hash_Additive2 | Multiplication by two big numbers, additive | 349 | 351 |
We’ve crossed an important threshold: the time of 327 ms corresponds to the simulation speed of more than 30K frames/sec. We started at 3.6K and set a goal of 10,000 frames/sec. We are now doing much better than that.
Different versions are the champions on different versions of Java. The division-based additive version performs best on Java 7, while the version based on multiplication by two big numbers works better on Java 8.
The ultimate additive implementation
The version based on multiplication by two big numbers allows yet another improvement. Currently, for the cell with the position (x, y) we keep both co-ordinates (as parts of one 64-bit number), and the hash value
where A and B are our constant factors. In our case N = 32, but we may use other values. Both the (x, y) pair and the hash value are updated when we move from a cell to its neighbour. But where are we using x and y?
Apart from calculating the new x and y and reporting the final result of the simulation, in one place only: comparing the cell’s position with the requested one in get().
If there was a one-to-one mapping between x and (Ax mod 2N)
(likewise, y and (By mod 2N)),
we wouldn’t need x and y at all. We could then store two values
y' = By mod 2N
and calculate hash quickly as
The mapping would allow us to recover x and y when we finally need them to get the simulation result. Before that, we can do without these variables.
Fortunately, such mapping exists. Our factors A and B are chosen as prime numbers, and a weaker condition is required for such mapping: for the numbers to be relatively prime with 2N, or, simply speaking, to be odd. All we need is to find the number A’, so that
Then
Before finding A’ and B’ we must decide on the value of N. It is attractive to set it to 32, but that will cause problems updating x’ and y’. We want to store them in two 32-bit parts of a 64-bit number and update with just one add operation. An overflow, however, may happen when we add or subtract B to the lower part. Previously we resolved this problem by adding offset of 0x80000000 or 0x8000000 to both parts. This prevented overflow when subtracting 1 from the value 0. An overflow might still happen when |y| is big, but this was considered unlikely for any realistic simulation.
Now we want to add or subrtact B = 7,436,369 to the lower part, and this can easily cause overflow. Just 288 such additions will outgrow 32 bits.
Here is the plan. We’ll set N to 31 and will keep the higher bits of both sides cleared. When applying negative offsets, we will add (−B & (231−1)) instead of subtracting B. This will avoid overflows at a cost of reducing our workspace to 31 bits instead of 32.
For our numbers
B = 7436369
we have, when N=31:
B' = 2058014897
The class AdditiveCell supports conversion from the traditional format to the hash-format:
public static long MASK = 0x7FFFFFFF7FFFFFFFL;
public static long encode (int x, int y)
{
return w (x * A, y * B) & MASK;
}
public static Point decode (long hash)
{
int x = (hi (hash) * Ar) << 1 >> 1;
int y = (lo (hash) * Br) << 1 >> 1;
return new Point (x, y);
}The change in the Life implementation is quite straightforward (see Hash_Additive3). Here, for instance, is new set() and new inc():
public static long AM = w (-AdditiveCell.A, 0) & MASK;
public static long BM = w (0, -AdditiveCell.B) & MASK;
void set (AdditiveCell c)
{
long w = c.pos;
inc (w+AM+BM);
inc (w+AM);
inc (w+AM+B);
inc (w+BM);
inc (w+B);
inc (w+A+BM);
inc (w+A);
inc (w+A+B);
c.set ();
}
private void inc (long w)
{
w &= MASK;
AdditiveCell c = get (w);
if (c == null) {
put (new AdditiveCell (w, 1));
} else {
c.inc ();
}
}The new hash function is worth looking at:
private int hash (long key)
{
return hi(key) + lo(key);
}We’ve almost returned to the starting point, when we used a Long object to represent our position, and that object’s hash function looked almost exactly like this.
The only difference is that previously the co-ordinates of adjoining cells differed by 1 and now they differ by A and B.
Here are the new results:
| Class name | Comment | Time, Java 7 | Time, Java 8 |
|---|---|---|---|
| Hash_Additive | The division-based hash function, additive | 358 | 327 |
| Hash_Additive2 | Multiplication by two big numbers, additive | 349 | 366 |
| Hash_Additive3 | Multiplication by two big numbers, ultimate additive | 343 | 361 |
The new additive solution is the best we’ve produced on Java 7. The additive division-based version is still the best for Java 8.
The summary
This is where our improvements end. Other data structures may produce better results, but our goal was to check how far we can get using a classic hash map.
Here is the entire change history:
| Class name | Comment | Time, Java 7 | Time, Java 8 |
|---|---|---|---|
| Hash_Reference | Initial version with a trivial hash function | 2763 | 4961 |
| Hash_LongPoint | Hash function changed to modulo big prime | 2032 | 1650 |
| Hash1 | Mutable Count | 1546 | 1437 |
| Hash2 | A unified hash map | 1309 | 1163 |
| Hash3 | Check in set removed | 1312 | 1151 |
| Hash4 | Entry iterator in the loop | 1044 | 976 |
| Hash5 | ArrayList<Entry> introduced | 1006 | 975 |
| Hash6 | Re-used ArrayList<Entry> | 1097 | 947 |
| Hash7 | ArrayList replaced with an array | 1020 | 904 |
| Hash8 | LinkedHashMap used, capacity made bigger | 843 | 591 |
| Hash_HomeMade | The first home-made hash map implementation (small capacity) | 513 | 465 |
| Hash_HomeMade2 | The hash map code is built into the main code | 479 | 449 |
| Hash_HomeMade3 | The cells are collected into a double-linked list | 480 | 433 |
| Hash_HomeMade4 | The hash map capacity is set to 256K | 405 | 353 |
| Hash_HomeMade5 | The action lists were introduced | 395 | 354 |
| Hash_HomeMade6 | The division-based hash function, hard coded | 392 | 353 |
| Hash_Additive | The division-based hash function, additive | 358 | 327 |
| Hash_Additive2 | Multiplication by two big numbers, additive | 349 | 351 |
| Hash_Additive3 | Multiplication by two big numbers, ultimate additive | 343 | 361 |
Here is the same data as a graph (the Java 8 time for Hash_Reference is excluded):
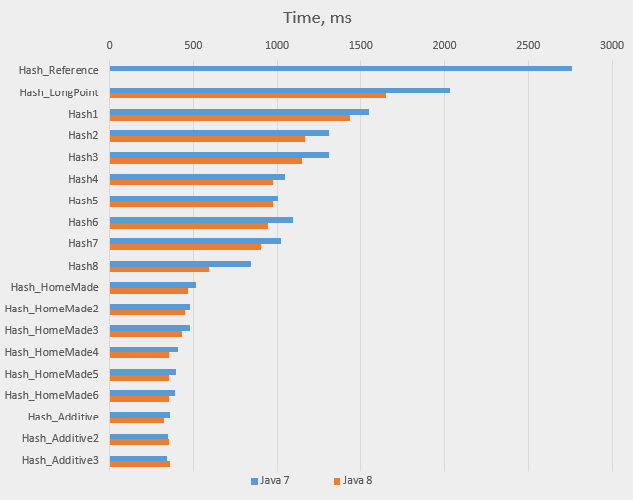
To see which changes gave the best effect, let’s draw another table, with improvements (in percents) over previous versions:
| Class name | Comment | Improvement, percent | |
|---|---|---|---|
| Java 7 | Java 8 | ||
| Hash_LongPoint | Hash function changed to modulo big prime | 26.46 | 66.74 |
| Hash1 | Mutable Count | 23.91 | 12.91 |
| Hash2 | A unified hash map | 15.33 | 19.07 |
| Hash3 | Check in set removed | -0.23 | 1.03 |
| Hash4 | Entry iterator in the loop | 20.43 | 15.20 |
| Hash5 | ArrayList<Entry> introduced | 3.64 | 0.10 |
| Hash6 | Re-used ArrayList<Entry> | -9.05 | 2.87 |
| Hash7 | ArrayList replaced with an array | 7.02 | 4.54 |
| Hash8 | LinkedHashMap used, capacity made bigger | 17.36 | 34.62 |
| Hash_HomeMade | The first home-made hash map implementation (small capacity) | 39.15 | 21.32 |
| Hash_HomeMade2 | The hash map code is built into the main code | 6.63 | 3.44 |
| Hash_HomeMade3 | The cells are collected into a double-linked list | -0.21 | 3.56 |
| Hash_HomeMade4 | The hash map capacity is set to 256K | 15.63 | 18.48 |
| Hash_HomeMade5 | The action lists were introduced | 2.47 | -0.28 |
| Hash_HomeMade6 | The division-based hash function, hard coded | 0.76 | 0.28 |
| Hash_Additive | The division-based hash function, additive | 8.67 | 7.36 |
| Hash_Additive2 | Multiplication by two big numbers, additive | 2.51 | -7.34 |
| Hash_Additive3 | Multiplication by two big numbers, ultimate additive | 1.72 | -2.85 |
The most productive ideas were:
- use of better hash function (26% on Java 7; 67% on Java 8)
- replacing the standard hash map with a specialised implementation (39%, 21%)
- using mutable objects instead of
Integers (24%; 13%) - iterating the map using
Entryobjects (20%; 15%) - using
LinkedHashMapinstead of a usualHashMapand increasing the capacity (17%; 34%) - applying the equivalent change to the specialised map (17%, 18%)
Some of these (LinkedHashMap, increased capacity, better hash function, Entry objects) fall into the category “Use the library classes properly”. The others illustrate
the idea “get rid of standard classes and implement everything yourself”. This idea can’t be recommended as a general programming practice. However, there are situations
when this is appropriate – when the ultimate performance is required. But even in these cases it is better to have a library-based implementation first, and use it as a
reference.
The glider gun
In the first article I mentioned the Gosper glider gun – a device that spawns gliders at regular intervals. Here it is:
This gun has the period of 30 – it creates a new glider (5 cells) every 30 steps. This means that the total size of the structure grows by about 1,600 every 10,000 steps. This is a big challenge for our program. Our algorithm processes one cell at a time, so the time is proportional to the number of cells. This means that no matter what we do, the simulation will slow down. On top of that, we expect relative slowdown, caused by three factors:
-
The hash tables in general behave worse when the number of entries increases, and we’ve removed the hash table resize.
-
The more living objects, the more expensive is the garbage collector (although it’s likely to make a difference only when the number of objects is several million).
-
Eventually the objects will not fit into the RAM cache.
Let’s run the simulation. We’ll use the fastest version that we’ve created so far (Hash_Additive) on Java 8, just we’ll increase the hash map capacity from 256K to 2M.
Each 10,000 steps we’ll print the time it took to perform these 10,000 steps and the total time, the size of the colony, the time per cell and the current memory use.
| Steps | Time for 10,000, sec | Total time, sec | Cells | Time per cell, ms | Memory, MB |
|---|---|---|---|---|---|
| 10,000 | 0.75 | 0.75 | 1,713 | 0.44 | 18.5 |
| 20,000 | 1,6 | 2,3 | 3,384 | 0.48 | 9.0 |
| 30,000 | 2,7 | 5,0 | 5,036 | 0.53 | 9.3 |
| 500,000 | 125 | 2,206 | 83,384 | 1.49 | 25.0 |
| 1,000,000 | 324 | 13,577 | 166,713 | 1.94 | 41.9 |
| 1,500,000 | 553 | 35,203 | 250,036 | 2.21 | 58.6 |
| 2,000,000 | 834 | 70,420 | 333,384 | 2.50 | 75.4 |
| 2,500,000 | 1,126 | 119,481 | 416,713 | 2.70 | 92.2 |
The good news is that we managed to run two and a half million iterations on a rather big structure. The maximal number of live cells was 416K, which is not bad. The memory consumption is also reasonable (92 megabytes these days can even be called “small”).
The bad news is that the progress slows down significantly as the structure grows. We started at less than a second for 10,000 steps, and ended up at 1,126 seconds for the same amount (18 minutes). Total time for 2,5M steps was 33 hours 11 minutes, which makes it difficult to track really big structures, such as here: https://www.youtube.com/watch?v=xP5-iIeKXE8. We really need something better for structures like this.
The “time per cell” column deserves special attention. It shows time, in milliseconds, it took to process 10,000 iterations, per live cell. We see that it grows as our simulation progresses. Here is the graph of this time over the number of steps:
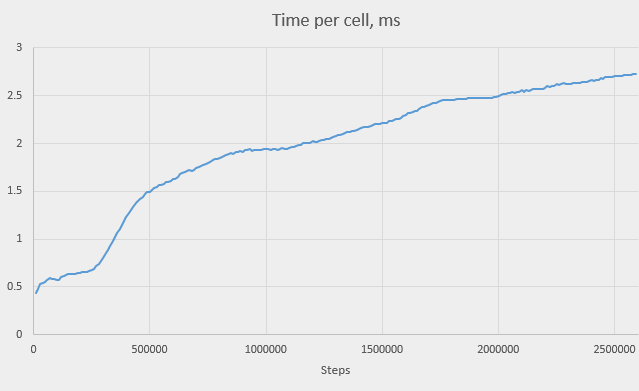
We see that the time per cell is indeed monotonously growing with the number of steps, but the growth rate isn’t always the same. There are even periods where the graph is nearly horizontal. In one place, however, the graph is very steep – just before step 500,000. The time nearly triples – it raises from about 0.5 ms to about 1.5 ms, reaching almost 2 ms at 1,000,000. We can explain this raise if we plot the time against the total memory use:
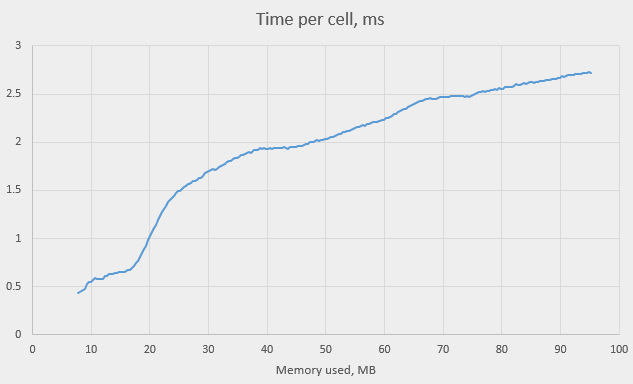
The steep portion of the graph corresponds to the memory consumption of 20M; the time keeps growing until memory reaches 40M. This is in agreement with the level 3 RAM cache of our machine being 20 MB. Our structure stopped fitting into the cache, that’s why the program slowed down. Again, as we saw in one previous study of the cache (How cache affects demultiplexing of E1 ), the cache miss penalty is relatively small – between 3 and 4 times instead of expected 10 – 20 times, despite our random memory access.
The time increase after that point is probably explained by another two factors (increasing garbage collector overhead and the hash map getting fuller).
A word about Life implementations
The point of this study was not to develop the fastest implementation of Life. It was to try hash tables for such implementation in a hope to learn something about them. It is clear that better data structures exist, it’s sufficient to look at the HashLife, which, despite the name, is much more advanced than anything we’ve produced.
If we concentrate on the simple and naïve Life implementations, the hash-based one has some advantages:
-
It is very simple to implement (even the most advanced of our implementations is very small in code size and quite readable).
-
It is not limited in space (or, strictly speaking, its space limits are rather wide), and, therefore, tolerates moving and expanding structures.
-
The number of live cells is only limited by the RAM size and can, therefore, be quite big on modern machines, although the program may become rather slow when this number becomes too big.
There are disadvantages, too:
-
It looks like processing of a single cell (looking up its eight neighbours in a hash map) is taking too long. The best speed we achieved was 0.44 ms per cell at 10,000 iterations, or 44 ns (114 CPU cycles) per one update of a cell. There must be faster ways.
-
Each cell (including dead cells with non-zero neighbour count) occupies quite a bit of space in memory (up to 36 bytes in a compressed-pointer mode and up to 52 bytes in a full 64-bit mode). In a matrix-based solution one cell can be stored in one bit.
-
A hash map is a non-local structure by design: the cells that are close to each other in Life space are not stored close in memory. This introduces bigger cache-miss penalties.
-
One cell is processed at a time; there is no low-level parallelism. We can’t use a longer register (such as a
long, or SSE/AVX) to process several cells at a time. -
The high-level parallelism (using several cores or even several hosts) isn’t easy to achieve either. A simple hash map isn’t suited well to be used by several threads. More complex data structures are required for that.
Conclusions
As said before, the true purpose of this story was to learn something about the hash maps and their use in Java. This is what we’ve learned:
-
The choice of a hash function is very important. If the source data were truly random, any reasonable hash function would work. However, the usual real-life data is non-random. The hash function must handle the real-life patterns in the incoming data.
-
In an application with heavy use of hash maps, the hash function is a really hot piece of code. A slow hash function can become a bottle-neck. A balance must be found between the speed of the hash function and its quality of hashing.
-
The hash map capacity is important. If the hash map isn’t iterated, consider giving it higher capacity (or a lower fill factor). If it is iterated, consider using a
LinkedHashMapclass and give it higher capacity also. Similar options must be considered for other implementations of hash maps, including custom-made ones. -
It is important to use the hash map optimally - for instance, use the
Entryobject where appropriate instead of re-invoking the hash map lookup. -
Updating mutable objects in hash maps is faster than removing and re-inserting immutable ones.
-
Implementing a custom hash map may be an option worth considering. Obvious considerations apply (the hash map must be a real bottleneck, all possible algorithm improvements already made, etc.). Just keep in mind that the library designer may improve the code in the next version, and the VM designers may introduce special treatment for this code. This means that the standard library may become faster than your custom-made code at any time. Constant performance monitoring is necessary.
-
The same applies to all the other standard classes (vectors, lists, etc.). In many cases implementing the functionality by hand can improve performance.
Coming soon
This is the end of the story of a hash-based Life implementation in Java. One thing that’s left is to try rewriting the code in C++ and checking which of the improvements are still applicable. This is what we’ll be doing next. Later we’ll also try to make a matrix-based Life implementation.