I finished my previous article with the observation that, despite the optimisation effort, the code generated by the GNU C compiler was still not optimal.
What’s wrong with the code?
Let’s concentrate on the Dst_First_3a.
class Dst_First_3a : public Demux
{
public:
void demux (const byte * src, unsigned src_length, byte ** dst) const
{
assert (src_length == NUM_TIMESLOTS * DST_SIZE);
for (unsigned dst_num = 0; dst_num < NUM_TIMESLOTS; ++ dst_num) {
byte * d = dst [dst_num];
for (unsigned dst_pos = 0; dst_pos < DST_SIZE; ++ dst_pos) {
d [dst_pos] = src [dst_pos * NUM_TIMESLOTS + dst_num];
}
}
}
};We compiled it with function alignment and loop alignment set to 32 and loop unrolling switched on. This is the assembly output:
_ZNK12Dst_First_3a5demuxEPKhjPPh:
subq $8, %rsp
cmpl $2048, %edx
jne .L40
xorl %r9d, %r9d
.p2align 5
.L28:
movq (%rcx,%r9,8), %rdi
movl %r9d, %edx
xorl %eax, %eax
.p2align 5
.L29:
movl %edx, %r8d
leal 32(%rdx), %r10d
movzbl (%rsi,%r8), %r11d
movb %r11b, (%rdi,%rax)
movzbl (%rsi,%r10), %r8d
leal 64(%rdx), %r11d
movb %r8b, 1(%rdi,%rax)
movzbl (%rsi,%r11), %r10d
leal 96(%rdx), %r8d
movb %r10b, 2(%rdi,%rax)
movzbl (%rsi,%r8), %r11d
leal 128(%rdx), %r10d
movb %r11b, 3(%rdi,%rax)
movzbl (%rsi,%r10), %r8d
leal 160(%rdx), %r11d
movb %r8b, 4(%rdi,%rax)
movzbl (%rsi,%r11), %r10d
leal 192(%rdx), %r8d
movb %r10b, 5(%rdi,%rax)
movzbl (%rsi,%r8), %r11d
leal 224(%rdx), %r10d
addl $256, %edx
movb %r11b, 6(%rdi,%rax)
movzbl (%rsi,%r10), %r8d
movb %r8b, 7(%rdi,%rax)
addq $8, %rax
cmpq $64, %rax
jne .L29
addq $1, %r9
cmpq $32, %r9
jne .L28
addq $8, %rsp
.cfi_remember_state
.cfi_def_cfa_offset 8
retLet’s look at the inner loop (the code between .L29 and jne .L29). This loop has been unrolled 8 times,
which corresponds to the following transformation of the original code:
for (unsigned dst_num = 0; dst_num < NUM_TIMESLOTS; ++ dst_num) {
byte * d = dst [dst_num];
unsigned dst_pos_x_32 = 0;
for (unsigned dst_pos = 0; dst_pos < DST_SIZE; dst_pos += 8) {
d [dst_pos + 0] = src [dst_pos_x_32 + 0 + dst_num];
d [dst_pos + 1] = src [dst_pos_x_32 + 32 + dst_num];
d [dst_pos + 2] = src [dst_pos_x_32 + 64 + dst_num];
d [dst_pos + 3] = src [dst_pos_x_32 + 96 + dst_num];
d [dst_pos + 4] = src [dst_pos_x_32 + 128 + dst_num];
d [dst_pos + 5] = src [dst_pos_x_32 + 160 + dst_num];
d [dst_pos + 6] = src [dst_pos_x_32 + 192 + dst_num];
d [dst_pos + 7] = src [dst_pos_x_32 + 224 + dst_num];
dst_pos_x_32 += 256;
}
}You can see that operation strength reduction has also happened: dst_pos * 32 became a separate variable,
updated once in the inner loop.
It is easy to see how registers are allocated:
%rsiissrc%rdiisdst%r9isdst_num%raxisdst_pos%edxisdst_pos_x_32
Here is the code for one assignment from the inner loop (after sorting out some instruction re-ordering):
leal 32(%rdx), %r10d
movzbl (%rsi,%r10), %r8d
movb %r8b, 1(%rdi,%rax)Why is there the leal instruction? All it does is that it adds 32 to %rdx and writes the result into %r10d.
The result of this addition is later used in the effective address of the movzbl, where another
register is added to it – %rsi (src). But wait, in Intel architecture an addressing mode can consist of
two registers (one possibly scaled) and an offset; why is this 32 offset not placed right there, like this?
movzbl 32(%rsi,%rdx), %r8d
movb %r8b, 1(%rdi,%rax)The hint comes from the name of the instruction (leal, rather than leaq), as well as the name of the result
(%r10d, rather than %r10): this is a 32-bit instruction. The %rdx is specified as an argument, but in actual
fact it only uses its lower 32 bits (%edx). Only the lower 32 bits of the result are used; they are written
into into %r10d, which is the low part of the 64-bit register %r10. The higher 32 bits are zeroed.
In short, the operation performs unsigned 32-bit addition (with possible wrapping in case of an overflow) and
converts the result to 64 bits. The leal here has nothing to do with “load effective address”, which is what its name stands for;
it is used as a replacement for the addition instruction (addl), for the only reason that it allows the result to be in
different register than the source, which saves a move instruction in our case. There is no way to combine this operation with a regular 64-bit addition in an
addressing mode.
Why is the compiler computing the sum in 32 bits?
The reason is simple: dst_pos is declared as unsigned, and unsigned, as well as int, is 32 bits long in GCC.
The %edx register corresponds to the dst_pos_x_32 variable from the pseudo-code, which equals to the
dst_pos multiplied by NUM_TIMESLOTS (32), and this is a 32-bit multiplication. Even if the
result is converted to a 64-bit value later, the C++ requires the multiplication to be performed in 32-bit
mode, and the high part of a result to be discarded. Check this:
unsigned x = 1000000;
unsigned long y = x * x; // result is 3567587328, which is
// 1000000000000L & 0xFFFFFFFFL
unsigned long z = (unsigned long) x * x; // result is 1000000000000In our example the multiplication was replaced with the addition (as a result of the strength reduction), but that addition was still performed in 32 bits for numeric safety:
addl $256, %edxThe same applies to adding of the offsets (32, 64, etc) to %edx: these must also be done in 32 bits.
If current value of %edx is close to 0xFFFFFFFF, adding 32 to it can cause
overflow and produce some small number as a result; this result would in fact be correct, while 64-bit result
(where no overflow occurs, and the result is big) would be incorrect. This means we can’t embed this addition into the addressing mode
of a load instructions, because address calculations are always 64 bits on this processor.
We know that in this loop dst_pos is actually small, and so does the compiler; that’s why it uses 64-bit register
(%rax) for this variable. It knows that no overflow can happen while adding 8 to it. However, it doesn’t seem to
be clever enough to figure out that no overflow happens while multiplying it by 32. That’s why it keeps dst_pos_x_32
in a 32-bit variable %edx and performs all the calculations with it in a 32-bit way, which is unsuitable for
effective address expressions.
Why are int and unsigned 32 bits?
C/C++ is quite relaxed about data type sizes. It requires int to be the same size as unsigned, both to
be at least 16 bits, both to be not smaller than short and not longer than long. I still remember compilers
where int was 16 bits, it was like that on all 8- and 16-bit platforms. 32-bit platforms established a new
standard, and for a long time the most common size of int has been 32 bits. The standard does not prevent
changing it to 64 bits.
I can think of two reasons why this hasn’t happened in GNU C. One is the legacy code. There is a huge amount of C code around, it is everywhere. Not all of it is well-written. Some of the code may contain dependencies on type sizes, and it is very difficult to find these dependencied in the code.
The other reason is that 64-bit isn’t always better. Unofficially C/C++ declares that int is the most natural
and the most efficient integer data format on the target architecture. We’ve seen that for the purpose of array indexing
the 64-bit type is indeed the most efficient. However, there are other cases.
First of all, the instruction encoding is implemented in such a way that the shortest instructions are 32-bit instructions
working with traditional registers (eax, edx, etc.):
01 C3 addl %eax, %ebx
48 01 C3 addq %rax, %rbx
this means that the 32-bit code is shorter. However, this is only applicable to small functions that can be fully
compiled using only traditional registers. As soon as the new registers (r8 .. r15) are used, the instructions
immediately become as long as in the 64-bit case:
49 01 C2 addq %rax, %r10
41 01 C2 addl %eax, %r10d
This means that the negative effect of working with 64-bit registers is relatively small for real programs.
There are 64-bit instructions that execute much longer than their 32-bit versions. Division is one example. Multiplication seems to run at the same speed.
64-bit numbers take twice the amount of space in data structures. It causes programs to use more memory and can reduce speed due to memory bandwith limitations.
32-bit numbers often allow better low-level optimisations than 64-bit numbers. Here is a simple example – a routine that adds two vectors of 256 numbers each. We’ll make two versions: for 32-bit numbers and for 64-bit:
void sum32 (unsigned *a, unsigned * b, unsigned * c)
{
unsigned i;
for (i = 0; i < 256; i++) a[i] = b[i] + c[i];
}
void sum64 (unsigned long *a, unsigned long *b, unsigned long *c)
{
unsigned long i;
for (i = 0; i < 256; i++) a[i] = b[i] + c[i];
}I won’t show the entire code here, it is surprisingly big
(you can see it in the repository).
I’ll only show the main loops. Here is one for sum32:
.L5:
addl $1, %esi
paddd (%r8), %xmm0
addq $16, %r8
cmpl %r9d, %esi
jb .L5And here is one for sum64:
.L17:
addq $1, %rsi
paddq (%r8), %xmm0
addq $16, %r8
cmpq %r9, %rsi
jb .L17The fragments look almost identical, except for one important difference: paddd instruction in the first case
and paddq in the second. These are the SSE-2 instructions.
Both operate on 128-bit xmm registers, but paddd
considers these registers consisting of four 32-bit words, while paddq of two 64-bit words.
The operations are performed simultaneously on all the components.
The code is really amazing. The GNU C compiler has a built-in vectoriser, which tries to use SSE wherever possible. In this case it has split a source vector into sub-vectors of sizes four or two, added those sub-vectors component-wise, and then calculated the sum of the result.
Obviously, the second code requires twice as many iterations, as a result it runs longer.
As you can see, there isn’t a simple answer to the question which integer type is the most natural on the Intel 64-bit architecture, and there are valid arguments both ways. However, it seems that 64 bits is the best size for values used to index arrays.
Going 64 bits
Let’s take Dst_First_3a and declare dst_pos a 64-bit variable. On the 64-bit GCC we can use unsigned long:
class Dst_First_3a : public Demux
{
public:
void demux (const byte * src, unsigned src_length, byte ** dst) const
{
assert (src_length == NUM_TIMESLOTS * DST_SIZE);
for (unsigned dst_num = 0; dst_num < NUM_TIMESLOTS; ++ dst_num) {
byte * d = dst [dst_num];
for (unsigned long dst_pos = 0; dst_pos < DST_SIZE; ++ dst_pos) {
d [dst_pos] = src [dst_pos * NUM_TIMESLOTS + dst_num];
}
}
}
};When we run it, we get the following:
12Dst_First_3a: 652
And the previous result we got (as published in “How to make C run as fast as Java”)
12Dst_First_3a: 727
We’ve got very significant improvement. It looks attractive to modify all the code in the same way.
Going portable
Replacing unsigned with unsigned long throughout the program seems a bit unsafe. What if it is bad for some
other platform? If some 32-bit platform defines unsigned long as 64-bit, such a modification will cause
a disaster. What we need is a special type for variables used as indices. Fortunately for us, such a type
exists, it is the size_t.
Strictly speaking, the size_t isn’t designed for indices, it is there for sizes. A sizeof operator returns
results of this type. Many library functions have parameters of this type: malloc(), calloc(),
memcpy(), qsort() and others. In addition to byte counts, it is used for element counts. It looks
very reasonable to use this type for indexing, as long as a programmer is happy to use an unsigned type. There
is a signed version of the size_t, too – it is called ptrdiff_t.
Our index variables are unsigned already, so we can make all of them size_t.
It makes sense to modify our interface and make src_length of type size_t as well. Besides making the code
consistent (we won’t compare size_t variables with unsigned), this has another positive effect: all the
versions that do not hard-code the input size will be able to work with any size that the platform allows.
Previously the input size was limited to 4 Gb, which for 64-bit platform is a totally unnecessary restriction.
Remember, when first talking about the type to use, in the article “De-multiplexing of E1 stream: converting to C”,
I mentioned size_t. I said then that I
was using unsigned, because size_t was also unsigned. I didn’t, however, use size_t itself, because I
considered it an unnecessary complication. Now it turned out that it was actually a performance feature.
This is how writing articles can help you learn something new.
This is what happens when we make everything size_t
(see the code in repository):
# c++ -O3 -falign-functions=32 -falign-loops=32 -funroll-loops -o e1 e1.cpp -lrt
# ./e1
9Reference: 1367
11Src_First_1: 987
11Src_First_2: 986
11Src_First_3: 1359
11Dst_First_1: 991
11Dst_First_2: 766
11Dst_First_3: 982
12Dst_First_1a: 763
12Dst_First_3a: 652
10Unrolled_1: 636
12Unrolled_1_2: 632
12Unrolled_1_4: 636
12Unrolled_1_8: 635
13Unrolled_1_16: 635
15Unrolled_2_Full: 635
The results look really impressive. Let’s put them into the table. The old results come from the previous article:
| Version | Time in Java | Old time in C | New time in C |
|---|---|---|---|
| Reference | 2860 | 1604 | 1367 |
| Src_First_1 | 2481 | 1119 | 987 |
| Src_First_2 | 2284 | 1101 | 986 |
| Src_First_3 | 4360 | 1458 | 1359 |
| Dst_First_1 | 1155 | 1079 | 991 |
| Dst_First_1a | 882 | 763 | |
| Dst_First_2 | 2093 | 880 | 766 |
| Dst_First_3 | 1022 | 1009 | 982 |
| Dst_First_3a | 727 | 652 | |
| Unrolled_1 | 659 | 635 | 636 |
| Unrolled_1_2 | 654 | 633 | 632 |
| Unrolled_1_4 | 636 | 651 | 636 |
| Unrolled_1_8 | 637 | 648 | 635 |
| Unrolled_1_16 | 25904 | 635 | 635 |
| Unrolled_2_Full | 15630 | 635 | 635 |
Observations:
-
All the versions became faster; some became much faster
-
All the unrolled versions now run at the same speed;
Dst_First_3aruns just a bit slower -
Even the
Referenceversion became very fast
The code
Let’s have a look at the code generated for Dst_First_3a
(the entire assembly output is in
the repository):
_ZNK12Dst_First_3a5demuxEPKhmPPh:
subq $8, %rsp
.cfi_def_cfa_offset 16
cmpq $2048, %rdx
jne .L40
xorl %r9d, %r9d
.p2align 5
.L28:
movq (%rcx,%r9,8), %rdi
leaq (%rsi,%r9), %rdx
xorl %eax, %eax
.p2align 5
.L29:
movzbl (%rdx), %r10d
movb %r10b, (%rdi,%rax)
movzbl 32(%rdx), %r8d
movb %r8b, 1(%rdi,%rax)
movzbl 64(%rdx), %r11d
movb %r11b, 2(%rdi,%rax)
movzbl 96(%rdx), %r10d
movb %r10b, 3(%rdi,%rax)
movzbl 128(%rdx), %r8d
movb %r8b, 4(%rdi,%rax)
movzbl 160(%rdx), %r11d
movb %r11b, 5(%rdi,%rax)
movzbl 192(%rdx), %r10d
movb %r10b, 6(%rdi,%rax)
movzbl 224(%rdx), %r8d
addq $256, %rdx
movb %r8b, 7(%rdi,%rax)
addq $8, %rax
cmpq $64, %rax
jne .L29
addq $1, %r9
cmpq $32, %r9
jne .L28
addq $8, %rsp
retThe code looks much better than before. Each line of the inner loop produces two instructions instead of three now:
movzbl 32(%rdx), %r8d
movb %r8b, 1(%rdi,%rax)Previously there were these three lines:
leal 32(%rdx), %r10d
movzbl (%rsi,%r10), %r8d
movb %r8b, 1(%rdi,%rax)In fact, the code looks close to ideal, To improve the speed even more, something extraordinary must be done.
By the way, the compiler chose different route from what I suggested before (adding an address, an index and an offset in the effective address calculation). It employed different transformation of the source program:
for (unsigned dst_num = 0; dst_num < NUM_TIMESLOTS; ++ dst_num) {
byte * d = dst [dst_num];
byte * s = src + dst_num;
for (unsigned dst_pos = 0; dst_pos < DST_SIZE; dst_pos += 8) {
d [dst_pos + 0] = s [ 0];
d [dst_pos + 1] = s [ 32];
d [dst_pos + 2] = s [ 64];
d [dst_pos + 3] = s [ 96];
d [dst_pos + 4] = s [128];
d [dst_pos + 5] = s [160];
d [dst_pos + 6] = s [192];
d [dst_pos + 7] = s [224];
s += 256;
}
}I don’t think this new way is any faster (after all, address modes are free), but it looks neater.
Retrospective
In “De-multiplexing of E1 stream: converting to C” we took a Java program and converted it into C++. Then we’ve done the following:
- configured function and loop alignment (article: The mystery of an unstable performance);
- optimised memory access to eliminate aliasing effects (article: How to make C run as fast as Java);
- configured loop unrolling (the same article)
- replaced
unsignedwithsize_t(today).
Here is a graph that shows how these steps affected the speeds of different versions:
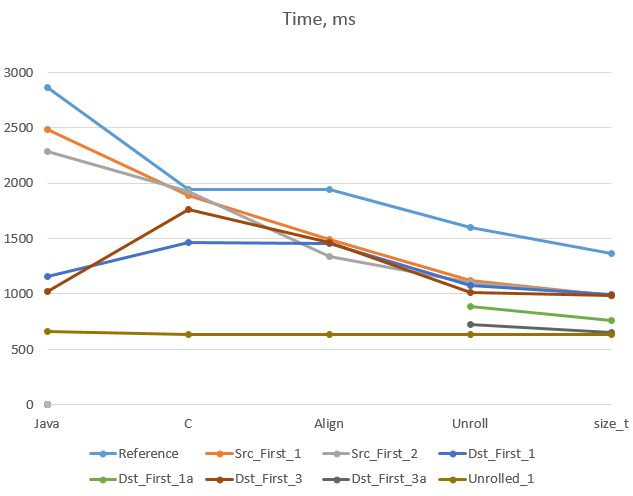
Conclusions
-
The size of the data types used does matter.
-
The type
size_tis there for a purpose; this purpose isn’t just for programs to look stylish and conform to the conventions – the programs really run faster if they use this type -
We have exhausted conventional ways of achieving high performance in C; further improvements require some radical change.
-
Although most versions now run much faster than their Java originals, the peak performance in C is the same as in Java.
-
GNU C isn’t a bad compiler after all
Coming soon
Until now all our versions were produced by direct translation form Java. Can we do better in some C-specific way? What if we sacrifice portability and write for the specific platform? Can we improve the speed this way? This will be the topic of my next article.